Предел функции - это фундаментальное понятие математического анализа, описывающее поведение функции при приближении аргумента к определенной точке. Рассмотрим основные методы вычисления пределов.
Содержание
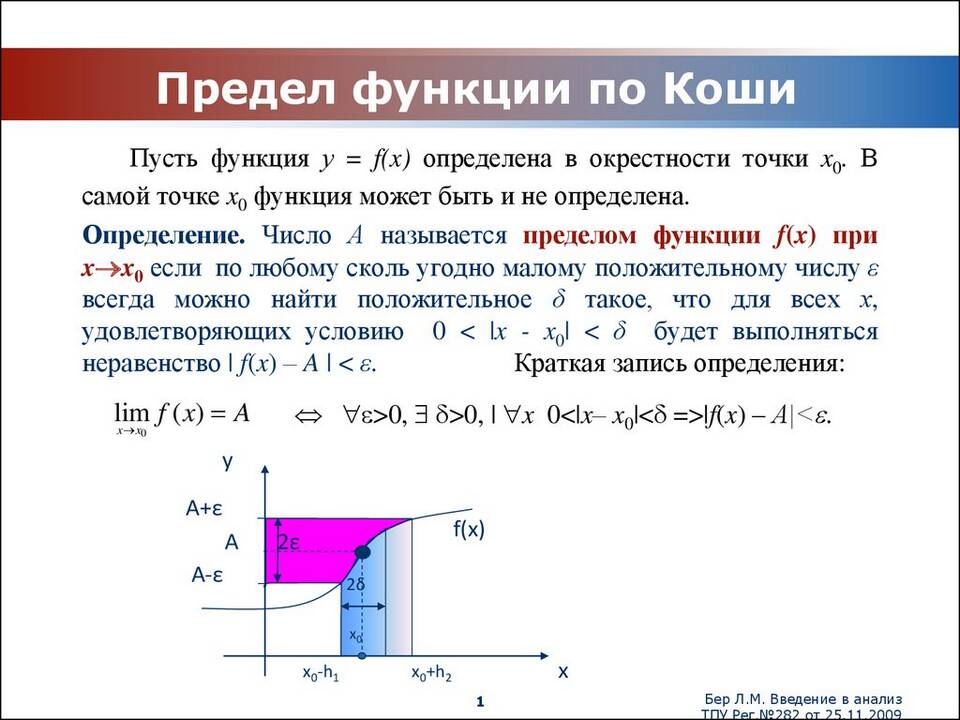
Основные определения
Предел функции f(x) при x стремящемся к a (обозначается limx→af(x)) - это значение, к которому приближается функция при приближении x к a.
Методы вычисления пределов
Непосредственная подстановка
- Подставьте значение a вместо x в функцию f(x)
- Если получается конечное число - это и есть предел
- Если получается неопределенность (0/0, ∞/∞ и др.) - используйте другие методы
Разложение на множители
- Применимо при неопределенности вида 0/0
- Разложите числитель и знаменатель на множители
- Сократите общие множители
- Повторите подстановку
Умножение на сопряженное
- Используется для иррациональных выражений
- Умножьте числитель и знаменатель на сопряженное выражение
- Упростите полученное выражение
- Вычислите предел
Таблица основных пределов
| Функция | Предел при x→0 |
| sin(x)/x | 1 |
| (1 + x)1/x | e |
| (ex - 1)/x | 1 |
Правила вычисления пределов
- Предел суммы равен сумме пределов
- Предел произведения равен произведению пределов
- Предел частного равен частному пределов (если предел знаменателя ≠ 0)
- Предел сложной функции: lim f(g(x)) = f(lim g(x))
Замечательные пределы
Первый замечательный предел:
limx→0 sin(x)/x = 1
Второй замечательный предел:
limx→∞ (1 + 1/x)x = e
Примеры вычисления
| Функция | Решение |
| limx→2 (x2 - 4)/(x - 2) | Разложим числитель: (x-2)(x+2)/(x-2) = x+2 → 4 |
| limx→0 (√(1+x) - 1)/x | Умножим на сопряженное: получаем 1/2 |
Вычисление пределов требует понимания основных методов и практики. Для сложных случаев могут потребоваться дополнительные техники, такие как правило Лопиталя или разложение в ряд Тейлора.