В геометрии существует несколько важных понятий, связанных с суммой в треугольнике. Наиболее известные из них - сумма углов треугольника и сумма длин его сторон (периметр). Рассмотрим эти понятия подробнее.
Содержание
В геометрии существует несколько важных понятий, связанных с суммой в треугольнике. Наиболее известные из них - сумма углов треугольника и сумма длин его сторон (периметр). Рассмотрим эти понятия подробнее.
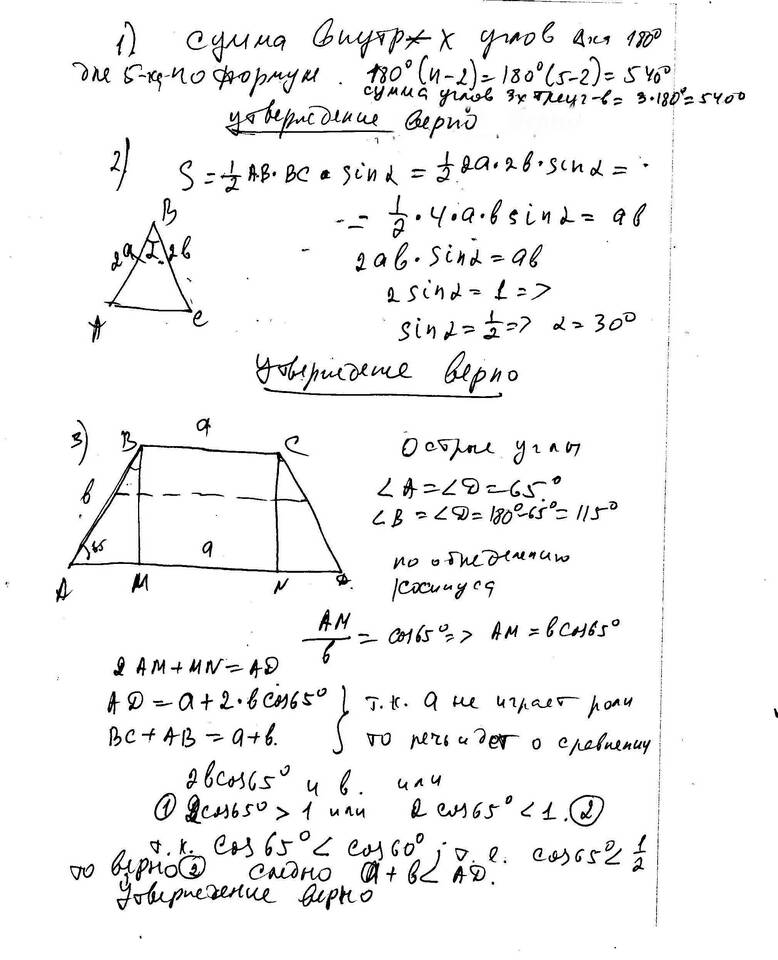
Сумма углов треугольника
Одно из фундаментальных свойств треугольников в евклидовой геометрии:
- Сумма внутренних углов любого треугольника всегда равна 180°
- Это свойство выполняется для всех типов треугольников: остроугольных, прямоугольных, тупоугольных
- Данное правило справедливо только для плоских треугольников на плоскости
Доказательство теоремы о сумме углов:
- Провести прямую, параллельную одной из сторон треугольника
- Использовать свойства параллельных прямых и накрест лежащих углов
- Показать, что три угла при вершине образуют развернутый угол (180°)
Периметр треугольника
Сумма длин всех сторон треугольника называется периметром:
| Формула | P = a + b + c |
| Где | P - периметр, a, b, c - длины сторон треугольника |
Особые случаи:
- Для равностороннего треугольника: P = 3a
- Для равнобедренного треугольника: P = 2a + b
Другие "суммы" в треугольнике
Сумма длин двух сторон
В любом треугольнике сумма длин двух сторон всегда больше длины третьей стороны (неравенство треугольника):
- a + b > c
- a + c > b
- b + c > a
Сумма квадратов сторон
В прямоугольном треугольнике выполняется теорема Пифагора:
a² + b² = c², где c - гипотенуза
Практическое применение
Знание сумм в треугольнике позволяет:
- Решать геометрические задачи
- Проверять возможность существования треугольника
- Вычислять неизвестные элементы фигуры
- Применять в строительстве и архитектуре
Пример задачи:
Два угла треугольника равны 45° и 60°. Найдите третий угол.
Решение: 180° - (45° + 60°) = 75°
