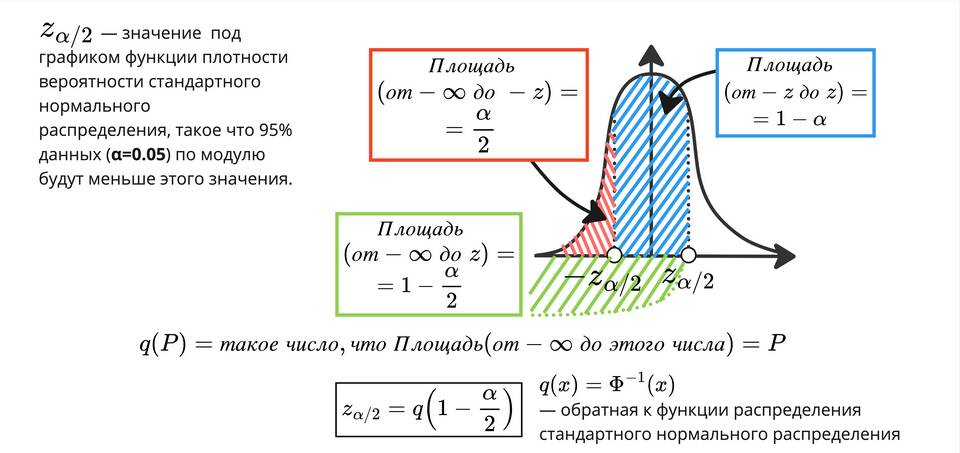
Доверительные границы представляют диапазон значений, в котором с определенной вероятностью находится оцениваемый параметр генеральной совокупности. Рассмотрим методы расчета доверительных интервалов для различных типов данных.
Содержание
Основные понятия
| Термин | Определение |
| Доверительный интервал | Диапазон значений, содержащий истинный параметр с заданной вероятностью |
| Уровень доверия | Вероятность (обычно 90%, 95% или 99%), с которой интервал содержит параметр |
| Стандартная ошибка | Мера изменчивости выборочной статистики |
Формулы для расчета доверительных границ
Для среднего значения (нормальное распределение)
Доверительный интервал = x̄ ± z*(σ/√n)
- x̄ - выборочное среднее
- z - критическое значение z-распределения
- σ - стандартное отклонение
- n - объем выборки
Для доли (биномиальное распределение)
Доверительный интервал = p̂ ± z*√(p̂(1-p̂)/n)
- p̂ - выборочная доля
- z - критическое значение
- n - объем выборки
Пошаговый алгоритм расчета
- Определите уровень доверия (обычно 95%)
- Выберите подходящую формулу в зависимости от типа данных
- Рассчитайте выборочную статистику (среднее, долю)
- Определите стандартную ошибку
- Найдите критическое значение распределения
- Вычислите границы интервала
- Интерпретируйте результаты
Критические значения для разных уровней доверия
| Уровень доверия | z-значение |
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
Пример расчета для среднего
| Параметр | Значение |
| Выборочное среднее (x̄) | 50 |
| Стандартное отклонение (σ) | 10 |
| Объем выборки (n) | 100 |
| 95% доверительный интервал | 50 ± 1.96*(10/√100) = [48.04, 51.96] |
Использование в статистических пакетах
- В R: функция t.test() или confint()
- В Python: scipy.stats.norm.interval()
- В Excel: ДОВЕРИТ.НОРМ() или ДОВЕРИТ.СТЬЮДЕНТ()
Факторы, влияющие на ширину интервала
- Объем выборки (увеличение n уменьшает интервал)
- Уровень доверия (более высокий уровень - шире интервал)
- Изменчивость данных (большее σ - шире интервал)